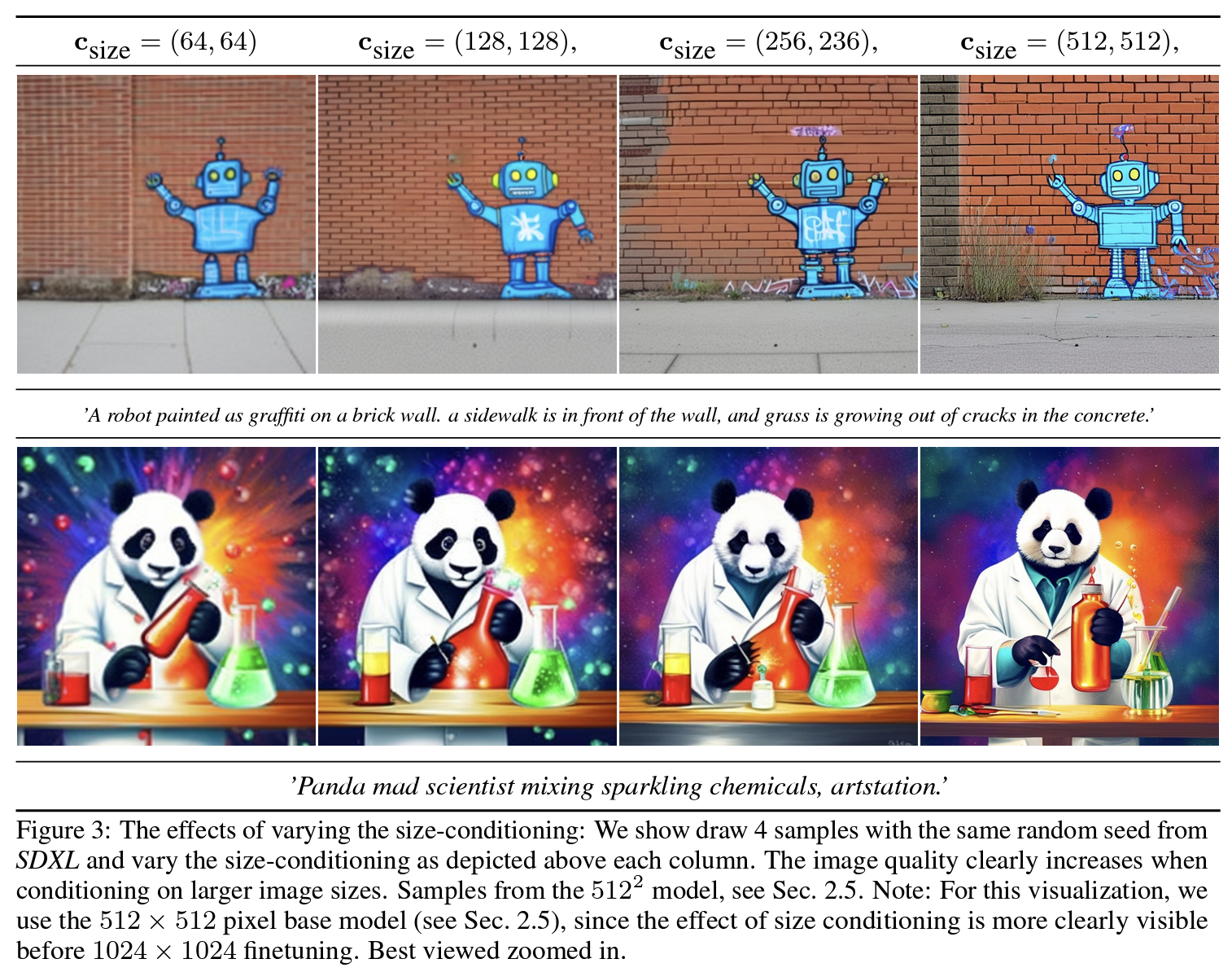
[Paper Review] VAE (Variational AutoEncoder)
Published:
This post is reviewing the VAE paper.
Citations
VAE : Auto-Encoding Variational Bayes - 논문 리뷰
Thumbnail image: towardsdatascience
Introduction
How can we perform efficient approximate inference and learning with directed probabilistic models whose continuous latent variables and/or parameters have intractable posterior distributions?
The answer lies in Variational Bayesian methods, which involve the optimization of approximations to intractable posterior probabilities.
Variational Bayesian (Appendix F)
Marginal Likelihood: The combination of KL divergence and the lower bound.
Variational lower bound to the marginal likelihood:
Monte Carlo estimate of the variational lower bound:
For more on Variational Bayesian methods.
Stochastic Gradient Variational Bayes (SGVB)
The SGVB estimator is a scalable estimator for variational inference that utilizes stochastic gradients, enabling optimization over large datasets. It facilitates efficient backpropagation through recognition models by approximating gradients, making it useful for efficient approximate posterior inference in almost any model with continuous latent variables and/or parameters.
Auto-Encoding Variational Bayes (AEVB)
The AEVB algorithm makes inference and learning particularly efficient by using the SGVB estimator to optimize a recognition model. This approach allows for very efficient approximate posterior inference using simple ancestral sampling, enabling the efficient learning of model parameters without the need for expensive iterative inference schemes like MCMC per datapoint.
Method
Problem Scenario
Considering the dataset below:
- The latent variable zi is generated from the prior distribution p_theta(z).
- The dataset xi is generated from the conditional distribution p_theta(x|z).
This approach addresses intractability (cannot compute marginal likelihood) and the challenge of large datasets (sampling should be conducted for each data point, which is costly for batch optimization).
The research proposes solutions for three problems:
- Efficient approximate ML or MAP estimation for the parameters theta. These parameters can be of interest themselves for analyzing natural processes and generating artificial data.
- Efficient approximate posterior inference of the latent variable z given an observed value x for chosen parameters theta. This is useful for coding or data representation tasks.
- Efficient approximate marginal inference of the variable x. This allows for various inference tasks where a prior over x is required, such as image denoising, inpainting, and super-resolution in computer vision.
To address these problems, the study introduces a recognition model q_theta(z|x) as an approximation to the intractable true posterior p_theta(z|x).
Method Summary
The recognition model parameters phi are learned together with the generative model parameters theta. Given a data point x, a stochastic encoder produces a distribution (e.g., Gaussian) of possible values for the code z that could generate x. A stochastic decoder p_theta(x|z) then produces a distribution of possible values of x given z.
The Variational Bound
Marginal Likelihood log(p_theta(xi)):
Right-hand side (RHS):
- KL divergence of the approximate from the true posterior (non-negative).
- L(theta, phi; xi), the variational lower bound on the marginal likelihood of datapoint i.
The objective is to differentiate and optimize the lower bound:
This corresponds to calculating the probability of x in Bayes’ theorem, known as the Evidence Lower Bound (ELBO). The loss function is derived from this ELBO.
The SGVB Estimator and AEVB Algorithm
Reparameterization Trick
Two assumptions needed to compute regularization:
- The distribution of z that emerges from passing through the encoder, q_phi(z|x), follows a multivariate normal distribution with a diagonal covariance matrix.
- The assumed distribution of z, the prior p(z), is that it follows a standard normal distribution with a mean of 0 and a standard deviation of 1.
KLD ensures these assumptions are met and facilitates optimization.
Thus, the approach is differentiable, enabling the calculation of regularization.
Variational Auto-Encoder (VAE)
The variational approximate posterior is a multivariate Gaussian with a diagonal covariance structure.
The log-likelihood log(p_theta(xi | z^(i, l))) is modeled as a Bernoulli or Gaussian MLP, depending on the data type.
Appendix C: MLPs as Probabilistic Encoders and Decoders
Bernoulli MLP:
Gaussian MLP:

Experiments
MNIST & Frey Face Datasets
Likelihood Lower Bound
Marginal Likelihood
Visualization of High-Dimensional Data
Conclusion & Future Work
The SGVB estimator and AEVB algorithm significantly improve variational inference for continuous latent variables, demonstrating theoretical advantages and experimental results.
Future work includes investigating the use of SGVB and AEVB in learning hierarchical generative models, particularly with deep neural networks such as convolutional networks for encoders and decoders. Additionally, applying these methods to dynamic Bayesian networks for modeling time-series data, extending the application of SGVB to optimize global parameters within models, and exploring supervised models that incorporate latent variables to learn complex noise distributions, enhancing model robustness and predictive performance.